The Geometry of Refusal

Nikit Phadke, a solo researcher, believes he’s developed a framework where AI hallucinations aren’t minimized… they’re mathematically impossible.

Not “statistically unlikely.” Impossible. Like dividing by zero.

That’s a huge claim and I was skeptical, but curious enough to pull the thread.

Evidence goes on a literal sphere. Admissible conclusions can only exist inside the geometric region that evidence defines. If your evidence contradicts itself, the region collapses. The system has to refuse. Not as a judgment call, but as a topological necessity.

One researcher. A Gmail address. No university affiliation. And an idea that’s either going to reshape AI safety or disappear into the arXiv graveyard. I spent a week trying to figure out which.

The Problem

Here’s the problem for AI in high-stakes domains. You build a system to approve mortgages. Or diagnose diseases. Or flag legal risks. And somewhere along the way, that system confidently says “approved!” when it absolutely should not have. The evidence didn’t support it. The policy didn’t allow it. But the model just… made it up.

This is expensive. In mortgage underwriting alone, we’re talking hundreds of millions annually in bad approvals. Nobody could figure out how to stop it architecturally. You could tune thresholds. Add guardrails. Pray. But the fundamental structure of these systems meant they could always, in principle, generate an answer that wasn’t supported by the evidence.

Nikit Phadke thinks he’s solved it.

The Core Insight

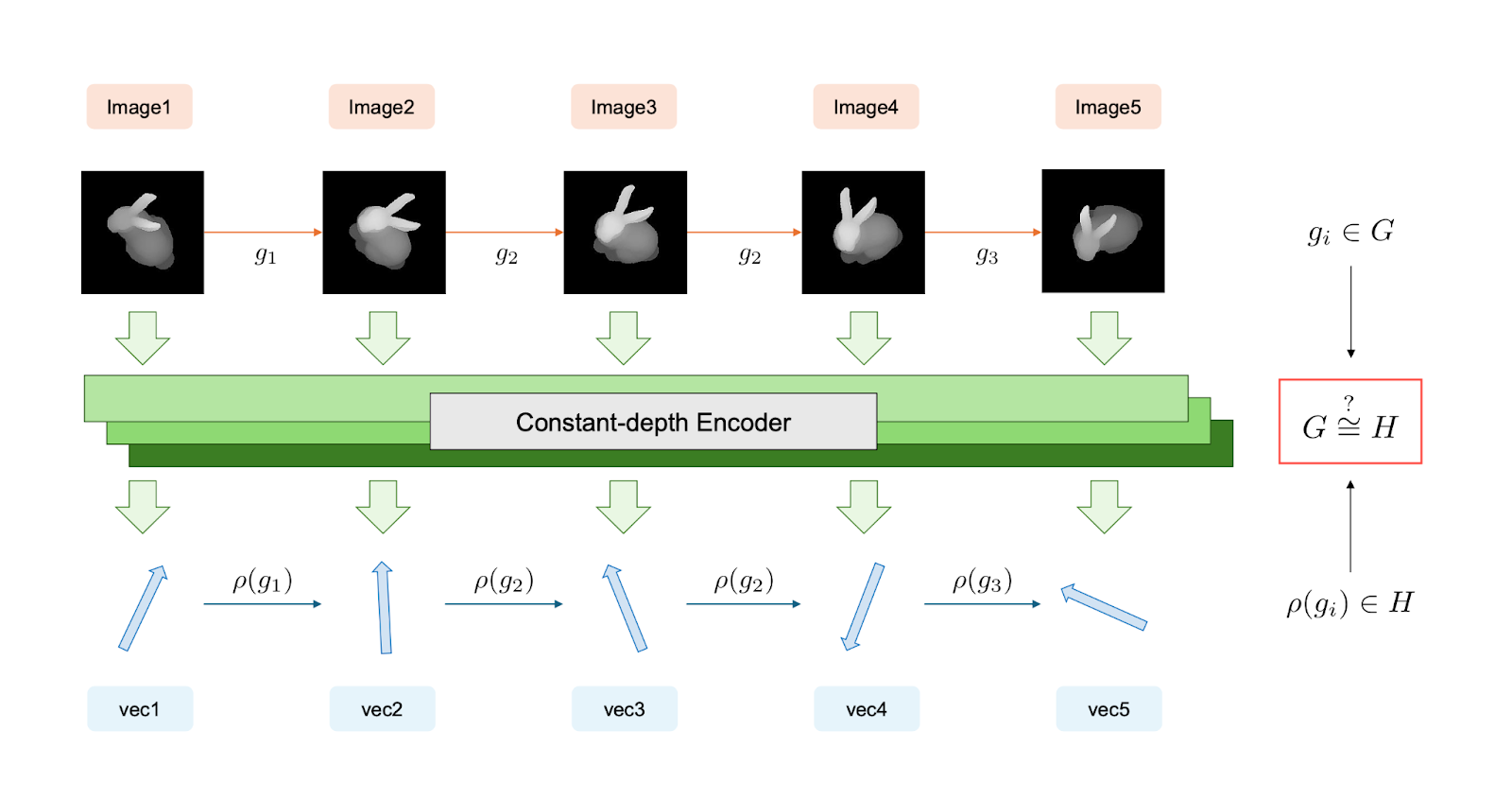
Traditional AI collapses everything together. Evidence. Policy. Decision. It all gets mashed into one learned function, and out pops an answer. The problem: once you do that, you can’t answer a simple question. Was this decision truly supported by the evidence, or did the model just interpolate something plausible?

Phadke separates these completely.

Evidence goes on a sphere. Not metaphorically — literally a high-dimensional sphere. Every piece of evidence becomes a point. The admissible region is the convex hull of those points. The only conclusions you can reach are the ones inside the geometric region your evidence defines.

Contradiction kills the region. When document A says one thing and document B says the opposite, traditional systems pick a winner or average them. In this framework, contradictory evidence spans more than a hemisphere. The admissible region collapses to nothing. The system must refuse. Not because a threshold wasn’t met. Because there’s no interpretation the evidence could possibly support.

Policy is a separate overlay. Want to change lending criteria from conservative to moderate? Don’t retrain the model. Swap the policy function. The evidence doesn’t move. Phadke proves (with theorems) that relaxing policy cannot admit interpretations outside the evidence region. You can change what you accept, but you cannot hallucinate new support.

Refusal becomes a geometric necessity, not a confidence heuristic.

Traditional AI mixes everything together. The geometric framework separates evidence (what’s true) from policy (what’s allowed), and only outputs interpretations the evidence actually supports.

The Test

The paper claims validation on “100,000 Freddie Mac mortgage loans” with “zero hallucinated approvals.” I emailed Phadke to ask what that actually means. He responded quickly. Here’s the reality:

Real: The loan characteristics (credit scores, debt-to-income (DTI) ratios, loan-to-value (LTV) ratios, repurchase outcomes) come from actual Freddie Mac data. When Freddie Mac flagged a loan as defective (meaning it never should have been approved), the system refused it. That’s real ground truth. Zero hallucinated approvals on loans that were historically repurchased.

Synthetic: The actual documents (the W-2s, bank statements, scanned PDFs) don’t exist. Due to personally identifiable information (PII) restrictions, no independent researcher gets access to real loan application packages without an institutional partnership. Phadke converted the real loan attributes into natural language statements (e.g., “Income has declined 25% from previous year”) and embedded those. Synthetic text assertions derived from real tabular data, not simulated document images.

So “zero hallucinated approvals” means: on synthetic text representations of real loan characteristics, the geometry worked as designed. The repurchase outcomes are genuine. The document processing layer is simulated.

That’s a valid proof of concept. It’s not “we deployed this at a bank.”

Even with the synthetic text caveat, one result stands out.

When policy relaxed from strict to moderate, 14 additional loans got approved. Legitimate loans that were geometrically admissible but outside the conservative threshold.

When policy relaxed further? Zero additional. They’d hit the geometric boundary. Nothing left in the admissible region.

The system found the actual edge of what evidence could support and stopped there. Not because it was trained to. Because the math demanded it.

That behavior (hitting a hard geometric wall rather than a fuzzy probability threshold) is the real demonstration. Even on synthetic text, it shows the architecture doing what Phadke claims.

Policy can expand, but it can’t exceed what evidence supports. When they relaxed from moderate to liberal, zero additional loans qualified. The system had already found the geometric edge.

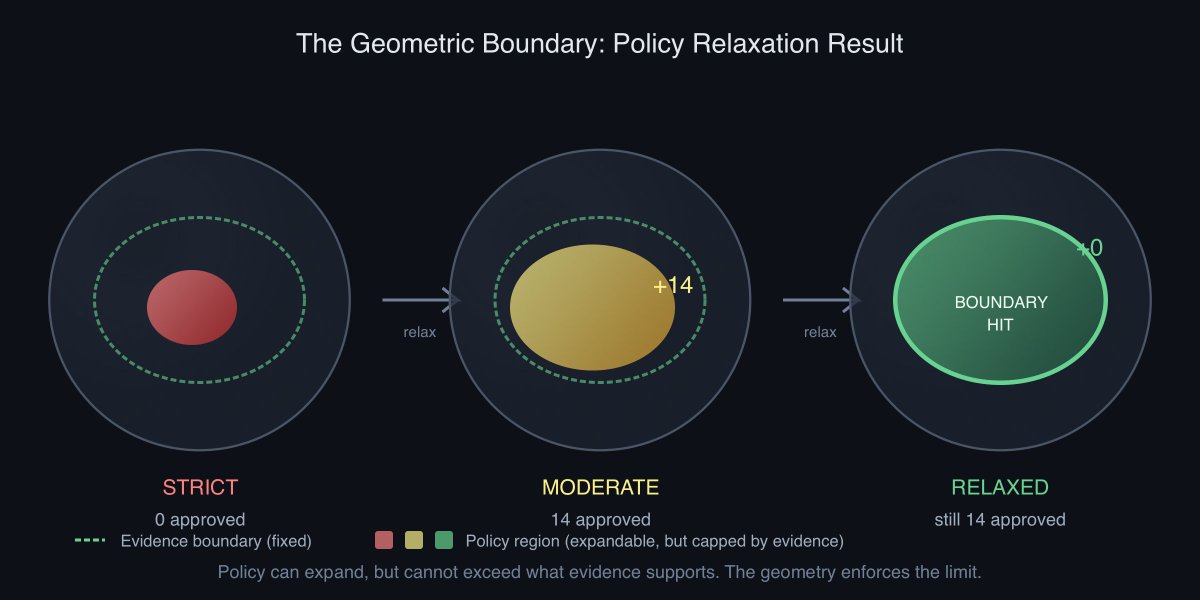
Policy can expand, but it can’t exceed what evidence supports. When they relaxed from moderate to liberal, zero additional loans qualified. The system had already found the geometric edge.

Open Vulnerability

I asked Phadke directly: what happens if the encoder screws up? The whole framework assumes you can accurately convert text into witness vectors. He uses SentenceTransformer.

His answer: “the error propagates.”

That’s honest. It’s also the weak link. The geometry is downstream of the embedding. If SentenceTransformer misreads a statement, the spherical hull is built on garbage. The math is perfect; the input pipeline isn’t.

He knows this. He’s working on “learned witnesses”: a custom embedder designed for this framework. But that’s future work, not current capability.

Theoretical Backstory

This paper is part of a larger research program. Phadke shared two supporting papers that explain the foundations:

REWA (Random-Embedded Witness Autoencoder): Phadke’s framework unifies Bloom filters, locality-sensitive hashing, Count-Min sketches, and transformer attention under one algebraic structure: functional witness projection over monoids. The paper proves that all these methods are instances of the same underlying mechanism, with complexity bounds of O(log N) for ranking preservation. If the proofs hold, that’s a genuine theoretical contribution.

Attention as Channel Decoding (from “Transformer Attention as a REWA Channel Decoder”): This supporting preprint derives that transformer attention is MAP decoding of a noisy similarity channel. The key result is Theorem 6.1, the “Sequence-Length Collapse Theorem,” which proves that a single attention head can reliably distinguish at most O(exp(sqrt(d))) keys. For typical head dimension d=128, this calculates to approximately 82,000 tokens — matching empirical observations of long-context transformer degradation in the 50k-100k range.

Both papers are currently in arXiv moderation, not yet publicly indexed. The math appears internally consistent across all three documents.

The Theorem

There’s a theorem buried in here that deserves its own attention.

Phadke proves you can only reduce uncertainty in two ways: add more evidence, or inject explicit bias. There’s no free disambiguation. Any system that always gives you an answer must be hiding bias somewhere. Only a system that can refuse maintains true neutrality.

This inverts everything about AI confidence. Traditional systems guess, then report how confident they are. This system determines what’s geometrically possible first, then generates only within that region.

Who Is This Guy?

Nikit Phadke. Independent researcher based in Pune, India. University of Utah background, tech/startup experience. Not an academic ML researcher. No institutional affiliation.

When I emailed questions, he responded same day with code links, supporting papers, and direct answers. Didn’t dodge the synthetic data question when pressed. GitHub repo (nikitph/bloomin) exists. Not a placeholder.

The vibe: sharp theorist who built what he could without institutional infrastructure, then described it in language that implied more than he had access to test. When asked about it, he clarified immediately.

What’s Still Missing

Peer review. None yet. He confirmed: “nothing has been reviewed so far.”

Real document validation. Someone with actual loan packages needs to run this on messy scanned PDFs, not synthetic text assertions.

Encoder robustness. The custom “learned witnesses” embedder is future work until it ships.

Adversarial testing. Can you inject contradictory witnesses on purpose to break the geometry?

Bottom Line

The theoretical framework is genuinely interesting. Separating evidence geometry from policy priors is a real architectural insight. The topological argument — that some inputs must be refused, not as policy but as mathematical necessity — is worth thinking about.

The validation is a proof of concept, not a production result. Real outcomes, synthetic text representations. The encoder is the weak link.

The claims in the paper oversell what was tested. “100,000 real-world financial decisions” should read “synthetic text assertions derived from real loan data.”

But the core idea? The geometry that forces refusal when evidence contradicts? The policy overlay that can’t manufacture support?

That’s not nothing. That might be something big, if someone with institutional resources picks it up and validates it properly.

A note about the author of the paper, Nikit Phadke: I contacted the author directly for this piece. An independent with bold claims in an era of AI generated papers… makes me suspicious. However, the math is not easy — even for an LLM. This is a rare level of understanding, especially for someone with a standard gmail address instead of something associated with a research institution. I am genuinely impressed with cross-domain synthesis and structure. I pressed him on the details; Nikit responded quickly, and competently. If you see proof to the contrary, please contact me with the details.

Sources:

• Paper: arXiv:2512.14731
• PDF: https://arxiv.org/pdf/2512.14731
• GitHub: https://github.com/nikitph/bloomin/tree/master/rewa_core
• GitHub: https://github.com/nikitph/bloomin/tree/master/adversarial-rewa-release
• LinkedIn: https://www.linkedin.com/in/nikitph/