The Bunny That Broke the Transformer

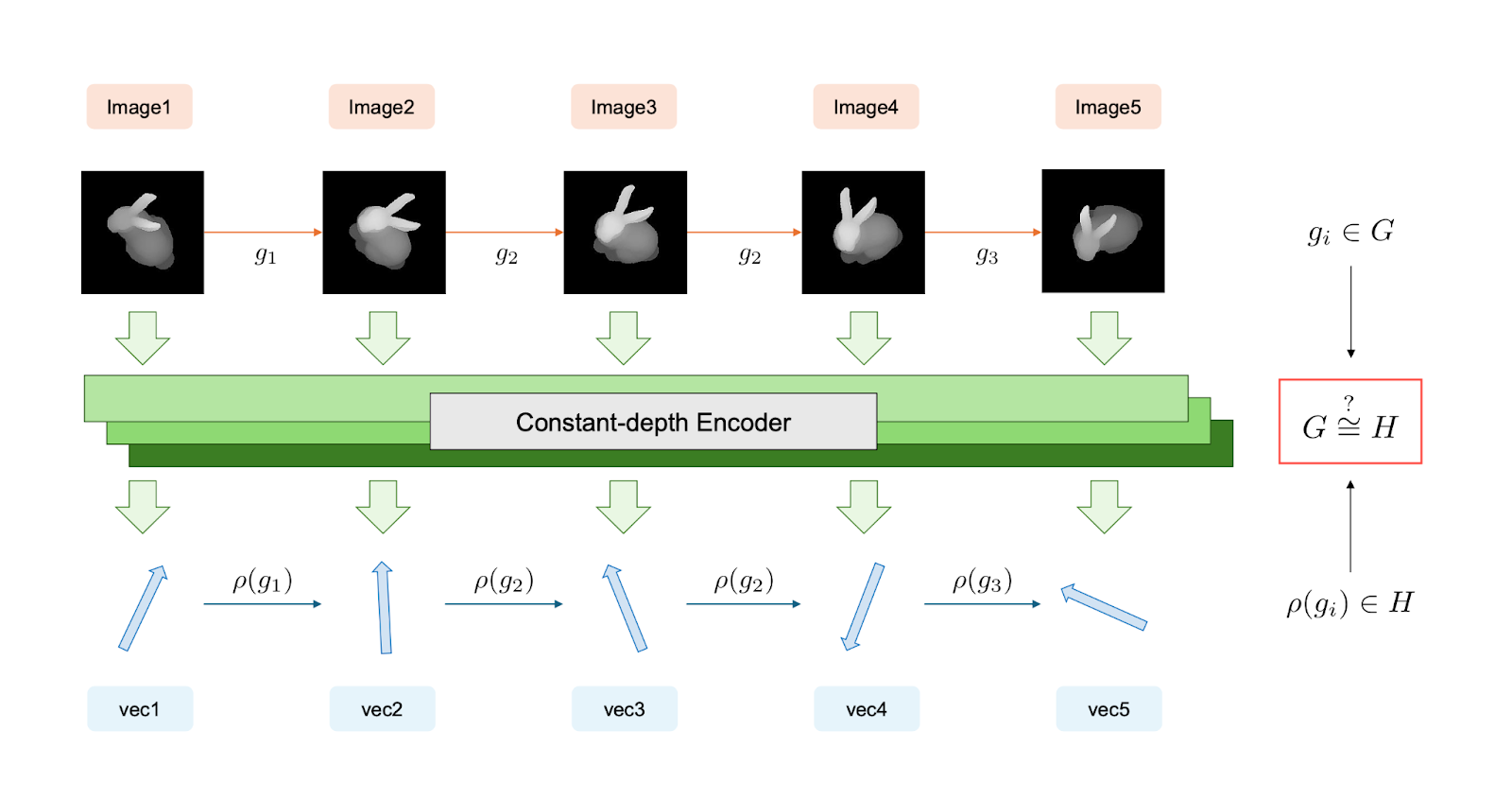
On a Monday in January, three researchers in Nanjing posted a paper with a rotating bunny on the first page. The bunny spins through five frames, ears tilting, body turning. Below it, a green bar labeled “Constant-depth Encoder.” Below that, vectors. The question in red: does the math inside match the motion outside?

The answer is no. And the paper proves it can’t.

Vision Transformers see the world as patches. Chop an image into 16x16 grids, embed each patch as a token, let attention flow between them. The architecture dominates computer vision. Classification, segmentation, multimodal alignment. Name a benchmark, a ViT probably tops it.

But there’s a pattern in the failures. Ask a model whether an object is left or right of another. Show it a shape, rotate it, ask if it’s the same shape or its mirror. Tasks that feel trivial. Tasks four-year-olds do without thinking.

The models fail. Not occasionally. Systematically.

The standard explanation: not enough data. Not enough scale. Train longer, train bigger, the failures will smooth out.

Siyi Lyu, Quan Liu, and Feng Yan asked a different question. What if the architecture itself is the ceiling?

To understand their answer, you need a detour through complexity theory. Not the hand-wavy kind. The kind with proofs.

Computational problems fall into classes based on the resources required to solve them. Two classes matter here: TC0 and NC1.

TC0 is the class of problems solvable by constant-depth circuits with threshold gates. Massive parallelism, shallow depth. Width scales polynomially with input size, but the number of sequential steps stays fixed.

NC1 requires logarithmic depth. Still parallel, but the circuit can grow deeper as the input grows. Problems in NC1 can chain dependencies. Step two depends on step one. Step three depends on step two. The depth scales with the problem.

The conjecture TC0 (strict subset of) NC1 says these classes are different. Constant-depth circuits cannot simulate logarithmic-depth circuits, no matter how wide you make them. The conjecture is unproven, but the consensus is P != NP level. If it’s wrong, most of what we think we know about computation is wrong.

Here’s the connection. Standard Vision Transformers, operating with fixed layers and polynomial precision, are bounded by TC0. Recent theoretical work has locked this down. Transformers excel at parallel pattern matching. They struggle with anything requiring sequential composition.

The Nanjing team formalized spatial understanding as a group homomorphism problem.

A group is a set of transformations with a composition rule. Rotate 30 degrees, then rotate 45 degrees, and you get a rotation of 75 degrees. The composition has structure. It follows laws.

For a model to truly understand spatial transformation, its internal representation must preserve that structure. If you rotate an object twice, the model’s latent space should reflect two rotations composed. This is what the paper calls a Homomorphic Spatial Embedding.

The question becomes: can a constant-depth encoder maintain this structure?

For simple transformations, yes. 2D translations are abelian. Order doesn’t matter. Translate left then up, or up then left. Same result. TC0 circuits can handle abelian structure.

But 3D rotation is different. The rotation group SO(3) is non-solvable. It contains subgroups where the Word Problem is NC1-complete. To track a sequence of 3D rotations, you need logarithmic depth. You need to chain dependencies.

Under the conjecture TC0 (strict subset of) NC1, constant-depth transformers cannot do this. Not “struggle with.” Cannot. The architecture lacks the logical depth to preserve the algebra.

The team tested it.

They built a benchmark called Latent Space Algebra. Three levels of difficulty, matched for visual complexity but separated by algebraic structure.

Level 1: 2D translation. Abelian. Move an object around a grid.

Level 2: Affine transformations. Scaling plus translation. Non-commutative but solvable. The group can be decomposed into abelian pieces.

Level 3: 3D rotation. Non-solvable. The theoretical barrier.

They tested ViT-B/16 (supervised on ImageNet), DINOv2 (self-supervised, explicitly trained to preserve geometry), and ResNet-50. Frozen weights. Linear probes trained only on single-step transitions, then tested on sequences of 2 to 20 steps.

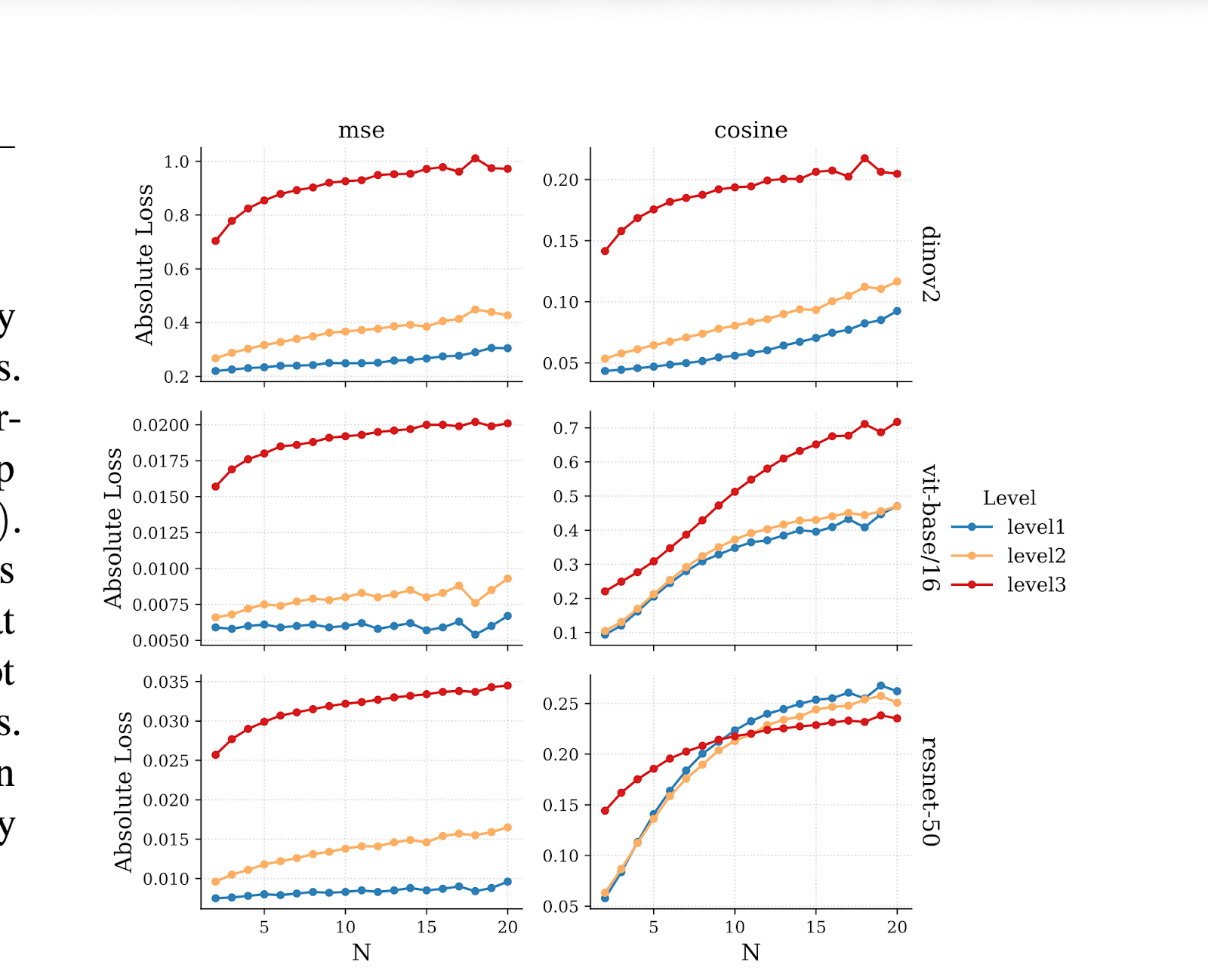
The results were stark.

On Level 1, errors grew slowly. The models could track translations over extended sequences.

On Level 3, errors compounded. By sequence length 9 or 10, the models performed worse than a baseline that simply guessed the object hadn’t moved. Prediction collapsed.

The gap between Level 1 and Level 3 was 3x to 3.8x in absolute error. Not a gradual degradation. A structural break.

The DINOv2 result matters most.

DINOv2 is trained without labels. Its objective encourages geometric sensitivity. If any vision model should preserve spatial structure, it’s this one.

It still failed on SO(3). The errors compounded at the same rate. The architectural ceiling held.

This rules out the training objective as the bottleneck. Supervised models failed partly because classification encourages invariance to translation and rotation. But DINOv2 doesn’t have that excuse. It was trained to care about geometry.

The constant-depth circuit is the ceiling. Not the loss function. Not the data. The architecture.

I emailed the corresponding author, Feng Yan, with three questions. He responded within a day, co-signed by first author Siyi Lyu.

On the TC0/NC1 conjecture:

“The separation between TC0 and NC1 is widely accepted in the theoretical community. While the consensus level is indeed similar to that of P != NP, the implications differ. This relationship fundamentally addresses whether there is a distinction between ‘parallel’ and ‘serial’ computation. If TC0 = NC1, it would imply that very shallow neural networks could perform tasks that strictly require deep processing. This would fundamentally overturn our current understanding of neural network architectures.”

On real-world failure modes:

“As the sequence of spatial group operations increases, the predictions of a network restricted to the TC0 complexity class will gradually drift. In autonomous driving, this manifests as risks in complex terrains involving intricate 3D relationships and during long-duration driving. We predict that current methods may produce significant deviations.”

On the path forward:

“This remains largely an open problem. Fixed-depth architectures struggle with long-sequence 3D spatial reasoning. However, simply increasing depth reintroduces historical challenges like training difficulties and error accumulation. Adding hard-coded inductive biases hampers generality. Hybrid architectures or new geometric modules might be the solution.”

This paper doesn’t stand alone.

A body of work is converging on the same conclusion through different angles. “The Illusion of State in State-Space Models” proves that SSMs, despite their recurrent formulation, hit the same TC0 ceiling as transformers. The “state” is an illusion. Mamba doesn’t escape the barrier.

“Circuit Complexity Bounds for RoPE-based Transformer Architecture” shows that rotary position embeddings don’t help. RoPE transformers with constant depth still can’t evaluate Boolean formulas.

“A Little Depth Goes a Long Way” demonstrates the positive case. Log-depth transformers can express sequential reasoning impossible for fixed-depth models. Depth is the lever, not width, not chain-of-thought.

The empirical failures follow the theory. LLMs struggle with parenthesis matching. Determining whether a sequence like (((())(())))((()) is balanced requires tracking nested state. NC1 territory. Models fumble it.

Knot untying is another test case. The KnotGym benchmark shows that model-based RL and chain-of-thought reasoning both fail at rope manipulation as complexity increases. Spatial reasoning that humans do without thinking.

The dilemma has no clean exit.

Fixed depth can’t solve non-solvable group structures. The proof is there.

Adding depth brings back the problems transformers were designed to escape. RNNs could chain dependencies, but they were unstable over long sequences. Vanishing gradients. Exploding gradients. Training pathologies that made them impractical at scale.

Hard-coding geometric structure, like SE(3)-equivariant networks, embeds the algebra into the architecture. But the non-solvable structure lives in fixed coefficients. The learnable dynamics remain bounded. And you lose generality. You can’t “automatically learn” spatial relationships if you’ve pre-specified the geometry.

The authors acknowledge this openly:

“Biological spatial perception differs significantly from our current paradigms. Humans perceive object constancy and handle knots and occlusions without complex, conscious reasoning. Continued cross-disciplinary thinking is essential.”

A four-year-old watches a toy rotate and knows it’s the same toy. No computation. No conscious tracking of axes and angles. The perception is immediate.

We don’t know how that works. We don’t know how to build it.

What we do know, now, is that the architectures dominating computer vision cannot learn it. The ceiling isn’t data or training or scale. It’s deeper than that.

The bunny keeps spinning. The models keep failing. The question of how to build systems that actually understand space remains open.

Sources:

• Lyu, Liu, Yan. “On the Intrinsic Limits of Transformer Image Embeddings in Non-Solvable Spatial Reasoning.” arXiv:2601.03048. January 2026.
• Author correspondence. January 9, 2026.
• Merrill et al. “The Illusion of State in State-Space Models.” arXiv:2404.08819.
• Chen et al. “Circuit Complexity Bounds for RoPE-based Transformer Architecture.” arXiv:2411.07602.
• “A Little Depth Goes a Long Way: The Expressive Power of Log-Depth Transformers.” arXiv:2503.03961.
• “Knot So Simple: A Minimalistic Environment for Spatial Reasoning.” arXiv:2505.18028.